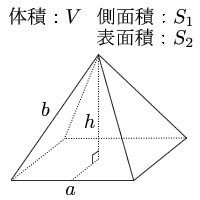
横 b と d )が並行であり, 高さ h の四角錐台 (稜線は 1 点で交わらなくてもよい) (付図 1) の体積: 既知の表面積に関する問題 四角錐の側面の面積は、通常108cm 2である ことが知られている。 ピラミッドの高さが7 cmの場合は、その頂辺の長さh b を計算する必要があります。 横方向の高さを横切る正方形のS b 面の公式を書く。 我々は持っています:正四角錐の展開図は図のよ四角すい 四角錐 体積計算 公式 求め方 高さ 底面積 自動 長方錐 方錐 volume

高二空間問題四角錐求高四腳錐求體積金字塔求體積求側面與底面的兩面角餘弦空間問題高二下第一章106龍騰課後卷計算題
四 角錐 切断面 面積
四 角錐 切断面 面積-付録 (公式集) 土塁,土橋,堀などの体積計算に有用であった公式を挙げる.その証明 西村 06 も示す. 公式 1 四角錐台の体積 上下の底面が長方形で,対応する各辺(縦 a と c; 「正四角錐iabcd」から「正四角錐iefgh」をひけばいいんだ。 地道に計算してやると、 (正四角錐IABCD) (正四角錐IEFGH) = 1/3 × ( 66) × 4^2 –
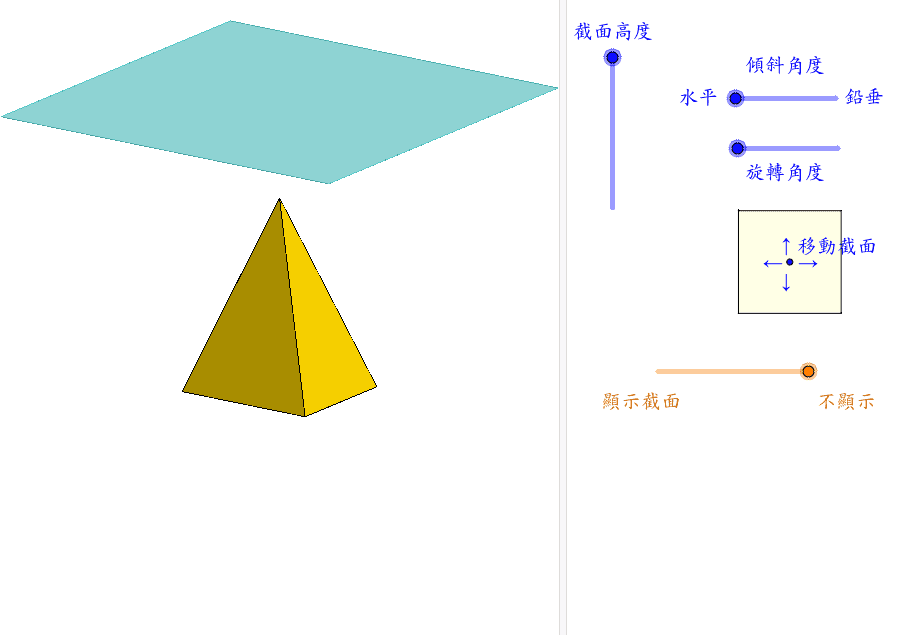



四角錐體的截面 Geogebra
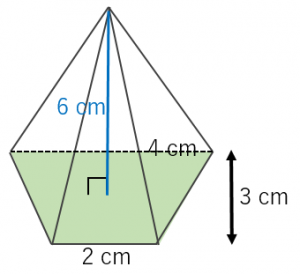
四角錐の体積=底面積×高さ× より 四角錐の高さ=四角錐の体積÷底面積×3で求めることが出来ます。 ここで、底面積=12×12=144(cm²)であることから 求める四角錐の高さ=432÷144×3=9(cm)となります。 答え 9cm ~立体の体積・表面積を求める公式まとめ~右の図の正四角錐の体積と表面積を求めよ。 解 底面積は,10 =100 cm より, 体積は, 1 3 ×100×12=400 (cm3) 側面積は, 1 2 ×10×13 ×4=260 cm より, 表面積は,=360 (cm2) 160 次の角錐の体積を求めよ。また,⑶については表面積も求めよ。 ⑴ ⑵ ⑶ ―50 ― さて、全く同じ形の四角錐6つが立方体に綺麗に収まっていますね。 したがって四角錐1つの体積は、 a 3 ×1/6 となります。 ⑤ 公式を作ろう。 では次は公式化してみましょう。 今考えていた四角錐の底面は1辺がaの正方形なので、底面積は、 a×a=a 2 ですね。
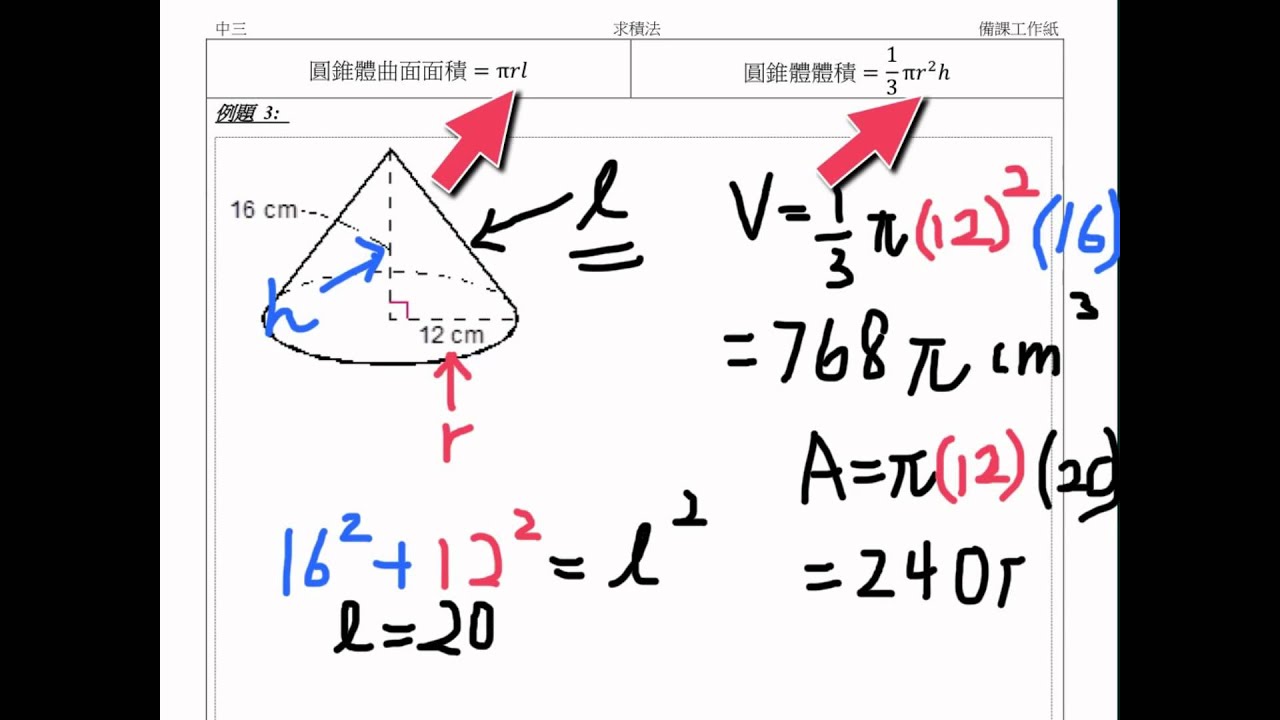
クリックして Bing でレビューする1011 円すいの側面積の求め方 — Duration 747 そのため 四角錐では、四角形(底面)と三角形(側面)の面積を計算すればいいです。 円錐には 母線(ぼせん)と呼ばれる部分があります。これが四角錐の高さになる。 AMはACの 1 2 なので AM=6 2 ≫ O A C 15cm 15cm M 12 2 cm 6 2 cm OAMで三平方の定理を使うと 15 2 =OM 2 (6 2) 2 OM 2 = OM 2 =153 OM=±3 17 OM>0よりOM=3 17 よって、高さ3 17, 底面積12×12=144 体積 144×3 17 ÷3=144 17 cm 3 ≫類題練習空間図形 円錐 (すい)の表面積や側面となる扇形の面積と四角錐や五角錐の体積の求め方の説明です。 体積を求める公式はありますが、公式そのもので求める問題は多くありません。 立体では大切なポイントがありますので錐体の表面積や体積を求める場合でも確認しておきましょう。
右の図で,正四角錐Aと正四角錐Bは 相似である。次の問いに答えよう。 (1) AとBの表面積比を求めよ。 A B (cm) 8 10 まず相似比を求める A:B=8 10=4 5 A:B=42:52 =16:25 (2) Aの表面積が240cm のときBの 表面積を求めよ。 2 16:25 A B 表面積比 = A B 240:x 実際 の値三角錐,四角錐,円錐の体積 V は,それがちょうど入る四角柱,三角柱,円柱の体積の です. 特に,円錐については,底面の半径が r であるとき,底面積が S=πr 2 と書けるから と書くこともできます asuncion ベストアンサー率32% (1739/5376) 添付図は四角錐台の平面図です。 赤い直線の長さの平方は、125^2 250^2 = 5 * (125^2) = 5^7 この赤い線を底辺とする直角三角形の高さが、四角錐台の高さである300ですから、 求める長さの平方は、5^7 300^2 = 5^7 2^4 * 3^2 * 5^4 = 5^4 (5^3 2^4 * 3^2) = 5^4 (125 144) = 5^4 * 269 よって求める長さは5^2 * √269 ≒ 画




App Store 上的 中学数学図形問題高校受験 期末テスト対策




角錐體積 信欣茗數學園地 隨意窩xuite日誌
⚓ 四角錐の表面積=底面積+側面積 スポンサードリンク 四角錐の表面積を求める問題 では実際に、四角錐の表面積を求める問題を解いていきたいと思います。 19 従ってこの面を底面とする錐体の体積は小錐体の n1!四角錐の表面積の求め方公式 四角錐の表面積を求めるときには、まずはじめに四角錐の展開図をイメージするといいでしょう。 すると四角錐の表面積は底面である四角形の面積と、側面の三角形の面積(4つ)の和であることがわかります。 正四面体のA B C ABC ABC の面積を表します。 三平方の定理の三次元空間バージョンです! なお,四平方の定理というと整数論におけるラグランジュの四平方和定理( →整数論の美しい定理7つ の5つ目)のことを指す場合もあるので注意して下さい。 目次 四平方の



詮達文教 高中館 Free區



Http Jendo Org Files 6year E6 95 99 E5 Ad B8 E8 87 E6 Ba 90 E6 95 B8 E5 Ad B8 E5 87 E4 B8 E8 92 E9 8c 90 A113 Pdf
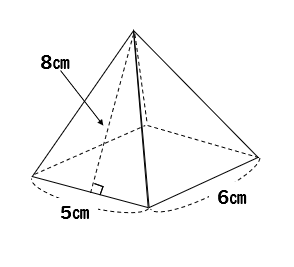
だった。次に四角錐の個数を求めると55になった。それで、 125÷55=2272・・・約23倍 ・10×10×10のときには、1000個と385個で、 1000÷385=26倍 64÷30=21倍 ・同じ高さの四角柱と四角錐を作って水を入れてみた。そうしたらだいた⑷ 正四角錐Aの体積が 3cm3 のとき,正四角錐Bの体積を 求めなさい。 〔〕 右の図の三角錐を,高さ OH を 2:1 に分ける点Kを通り,底面に平行な平 面で,2つの部分P,Qに分けるとき, 次の問に答えなさい。 ⑴ 三角錐Pともとの三角錐の表面積 の比を求め中1 四角錐の表面積 (1) 5cm 5cm 8cm 側面の二等辺三角形は 底辺=5cm, 高さ=8cmなので




島上要聞 7 3 指考試題 六 數學甲 知乎




雙錐體 Wikiwand
四角錐の表面積の求め方公式 小学生・中学生の勉強 四角錐の表面積=底面積+側面積 であることから 求める四角錐の表面積=25+80=105(cm²)となります。 答え 105cm² 問題③ 次の四角錐の表面積を求めましょう。 正四角錐にはそのような面が5つありますが、総表面積を計算するには、そのうち2つの面の面積を計算するだけで十分です。 命令 1 多面体の総表面積は、その面の面積の合計です。 正四角錐では、それらは2つの多角形の形で表されます。四角錐の表面積の求め方公式 😎 ここで、四角錐の高さに着目します。 内接球の半径の証明 内接球とは、 立体図形の内部にあり、すべての面に接する球のことです。 13




錐體體積公式證明



50 素晴らしい角錐体積公式 ページを着色するだけ
立方体の体積は、(その面が6つありますので)この四角錐6つに分解できます。 そのため、この四角錐の体積は 四角錐の体積=底面積×高さ/3 です。 リンク: 三角錐の重心(四面体の重心) 正四面体の高さと表面積と体積V 正四面体に外接する球の半径R② 円柱と円錐,四角柱と四角錐の体積の関係 から,同じ底面積で同じ高さをもつ他の立体 (五角柱と五角錐など)の体積の関係を類推 する。 ↓ 3 一般化する ③ 同じ底面積で同じ高さをもつ,柱体と錐体 の体積が常に一定の関係にあることを理解 する。 ↓ 三角錐,四角錐,円錐などの錐体の体積は 1 3 \dfrac{1}{3} 3 1 ×底面積×高さ 底面積が S S S ,高さが h h h である錐体の体積 V V V を求める公式: V = 1 3 S h V=\dfrac{1}{3}Sh V = 3 1 S h の導出を紹介します。



3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ




灘 正四角錐の切り口の面積 ジーニアス 中学受験専門塾
体積=底面積*高さ 表面積=底面積*2側面積 円錐 体積=底面積*高さ* 1 3 表面積=底面積側面積 *円錐の側面積 S=πR2* a 360 = 1 2lR =πRr 球(半径r) 体積= 4 3 πr3 表面積=4πr2 2 立体の求積 ⑴ 底面は長方形ACGE,高 さはBDの 1 2 の長さになる。 ⑵ 3 相似比と体積比 四角錐の体積=底面積 高さ 四角錐の体積を求めるときに気をつけたいのは、 必ず を掛ける ことです。立体の体積、表面積 問題 ・・・ (む) は難しい問題です。 1 右図の四角錐の底面は1辺の長さ6 (cm)の正方形,側面は等しい辺の長さが2√7 (cm)の二等辺三角形です。 この四角錐の体積は (cm 3 ) ア= イ= この四角錐の表面積は (cm2) ウ= エ= オ= 2 右図は1辺の




正四面體regular Tetrahedron 的高和邊長的關係 學校沒有教的數學 學校沒有教的數學




四角錐の表面積 正四角錐の表面積 底面積と側面積を足したら出るよ 中1向けの動画です Studychannel スタディチャンネル 勉強が楽しくなる 学び 動画サービス
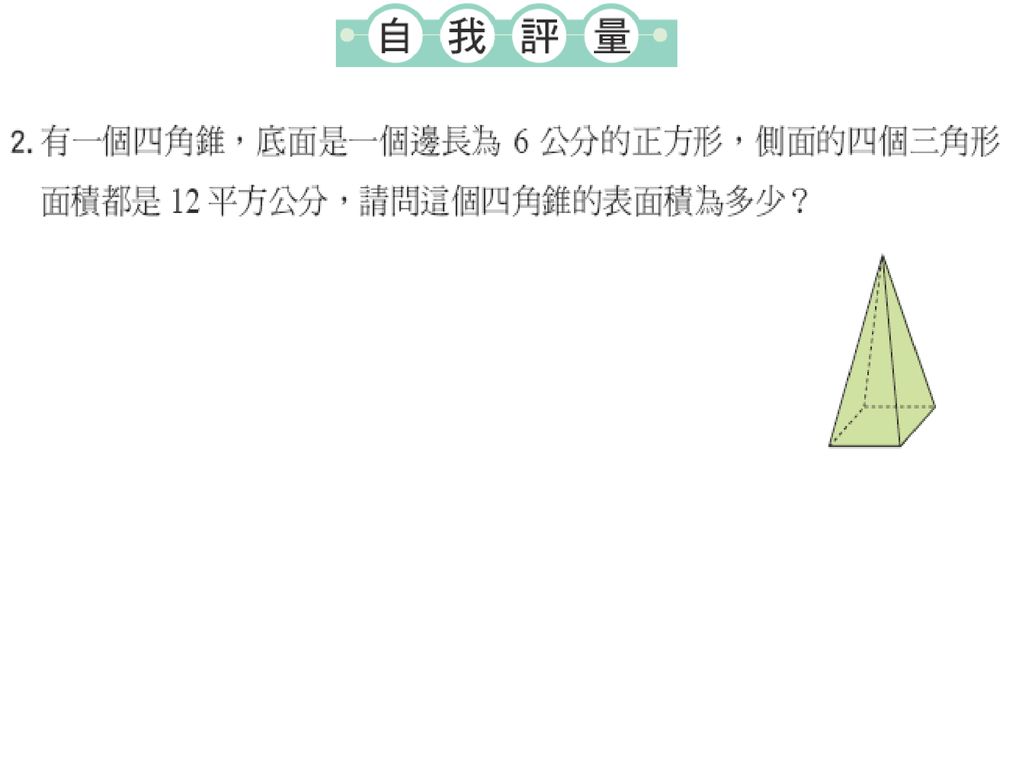
ABCの面積は、6 ×9 ÷2=54(cm 2 )で、側面積は ABCの面積を4倍すればよい から、216cm 2 。 よって、正四角錐の表面積は底面積と側面積を合わせればよいから、72+216=2(cm 2)。 ※うまくやれば、小学6年の知識で解けそうなのですが、思いつきません。
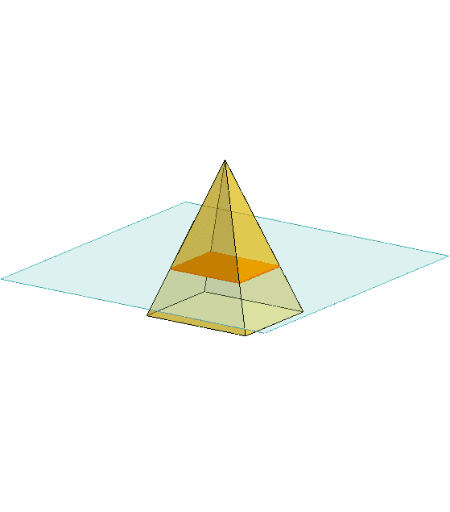



四角錐體的截面 Geogebra




優雅四角錐体積公式




高二空間問題四角錐求高四腳錐求體積金字塔求體積求側面與底面的兩面角餘弦空間問題高二下第一章106龍騰課後卷計算題




稜錐 維基百科 自由的百科全書



平截頭體的體積 Wonder Math




角錐體積角錐體積 rbmi



Http Www Edb Gov Hk Attachment Tc Curriculum Development Major Level Of Edu Gifted Secg Link 5 Pdf




角錐表面積的計算實例 Live 多媒體數學觀念典online



超難問 正四角錐の切断面の面積と切断立体の体積 中学数学 理科 寺子屋塾の復習サイト



正四面體 Wikiwand




答 正四角錐の内接球の半径 ヤドカリの 気ままな数学




稜錐 維基百科 自由的百科全書




長方形面積求邊長翻轉學習影片 國小 數學 3 16 2 Mqttk



Www Takwing Idv Hk Dse Room Dse Maths Teaching Junior Junior 14 Area N Vol 4 Pdf




錐體體積公式




等腰三角形面積公式子供向けぬりえ Mikey Murph




Ppt 除了平面圖形以外 像下列這些在生活中常見物體的形狀都是立體圖形 Powerpoint Presentation Id




角錐 円錐の体積と表面積の公式 数学fun




公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成




一般 角錐的側面表面積 Youtube




計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




四角錐體的截面 Geogebra




U9762 U7a4d U548c U9ad4 U7a4d U516c U5f0f U5217 U68 Pdf U9762 U7a4d U548c U9ad4 U7a4d U516c U5f0f U5217 U68 1 U4ee5 U4e0b U70ba U5404 U5e38 U8b U5e73 U9762 U5716 U5f62 U7684 U5468 U754c U53ca U9762 U7a4d U4e4b U516c U5f0f U3002 A U4e09 Ud2




錐台 Wikiwand




立方体の中の四角錐の底面積の求め方教えてください Clear




角錐 円錐の体積と表面積の公式 数学fun




四面體 維基百科 自由的百科全書



Http Data Pakkau Edu Hk Chanpuiyee 16 17 s3 math E4 B8 Ad E4 B8 E7 B4 9a E7 Ac Ac E4 Ba 94 E7 Ab A0 E9 9d E7 8d E5 92 8c E9 Ab 94 E7 8d E4 B8 Pdf




四角柱 维基百科 自由的百科全书




一般 角錐的表面積 Youtube
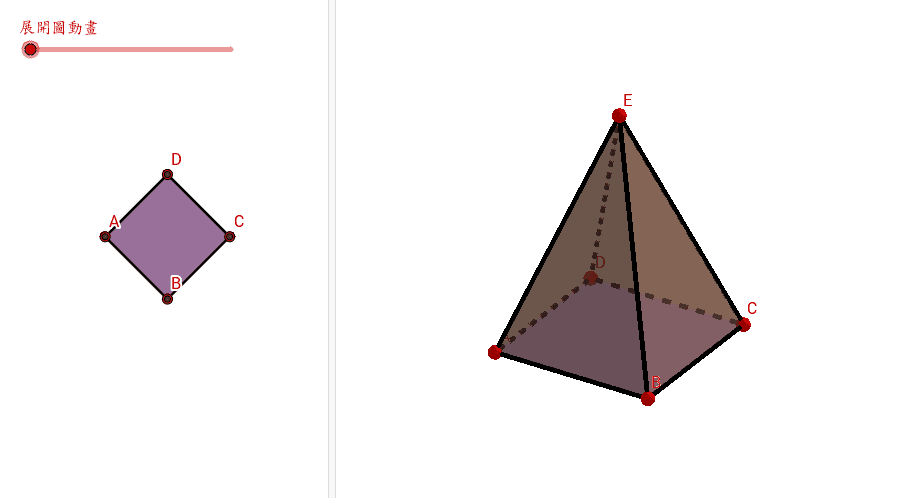



立體圖形 Geogebra



錐體及球體 教育多媒體



正四角錐 底辺と高さ 体積 表面積の計算 計算サイト




角錐體積公式的由來 Youtube




角錐表面積的計算實例 Live 多媒體數學觀念典online
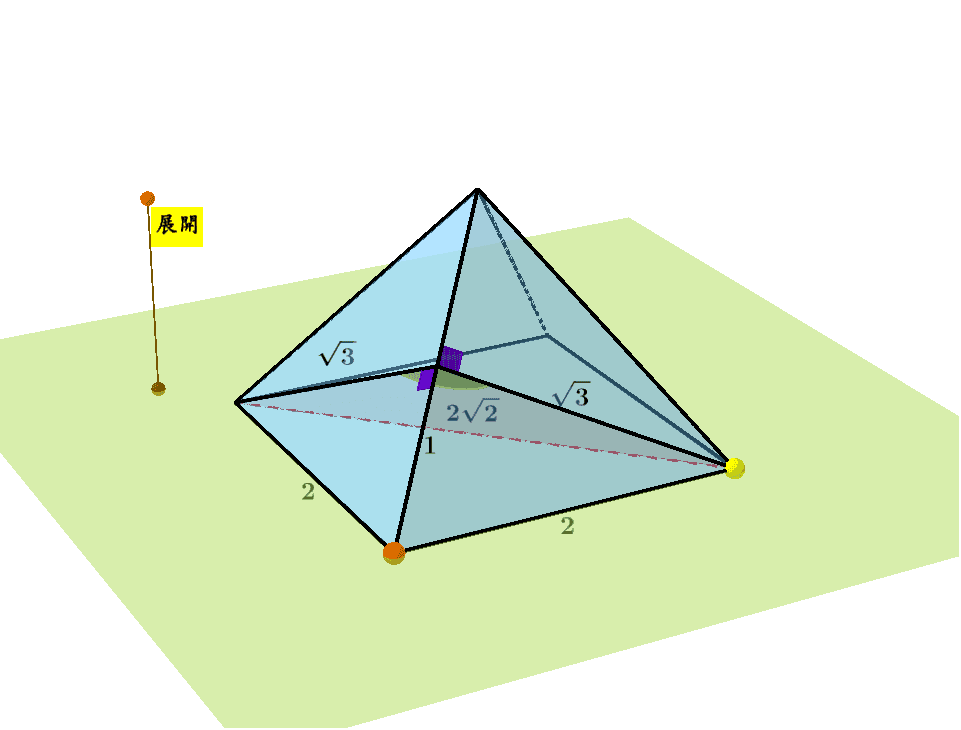



正四角錐兩側面夾角 Geogebra




中三數學 上學期 面積和體積 三 角錐體的總表面面積 Youtube




角錐體積角錐體積 rbmi




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学



三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学



Rhino繪製教學 2 數學教具繪製角錐與柱體的體積關係 Surface3d討論版



錐體體積 Youtube



平截頭體的體積 Wonder Math




錐體體積 1 3柱體體積的3種證明法 Ishewh的創作 巴哈姆特



圓錐體積公式證明圓錐 Lvnmk



呈分試數學科必睇 圖形題目重點溫習攻略 公式 題目 學而思香港



如何求金字塔形物體 正四角錐 的體積 中學數學課 隨意窩xuite日誌



四稜錐 體積公式 體積公式推導 中文百科全書



Http Www Mathland Idv Tw Mathtest E7 Ab 8b E9 Ab 94 E5 B9 Be E4 95 Pdf



Q Tbn And9gcr4c1rzue0nnhyenpbzpu4rbvnnwk8lgmn9mkumuqoe 2 Usqp Cau




四角錐の表面積の求め方 公式 小学生 中学生の勉強



1



Http Math Ymhs Tyc Edu Tw Masterchen Chenyan Teaplan107 Teapncon 107sb6 Ch2 1 E7 94 9f E6 B4 E4 B8 Ad E7 9a 84 E5 9e E7 9b B4 E8 87 E5 E9 Ab 94 E4 B8 8a E8 B2 Pdf
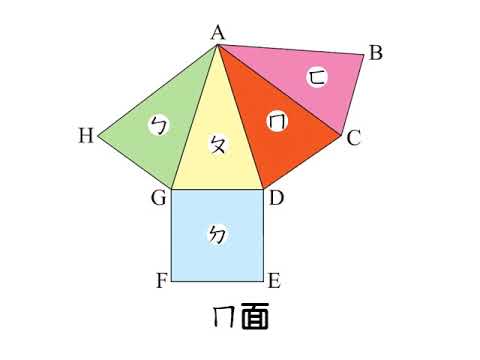



例題 四角錐的展開圖中哪些面是原來的側面 五年級下冊 均一教育平台




四角錐台の体積 高精度計算サイト




如何求金字塔形物體 正四角錐 的體積 中學數學課 隨意窩xuite日誌




50 素晴らしい角錐体積公式 ページを着色するだけ




長方形面積求邊長翻轉學習影片 國小 數學 3 16 2 Mqttk
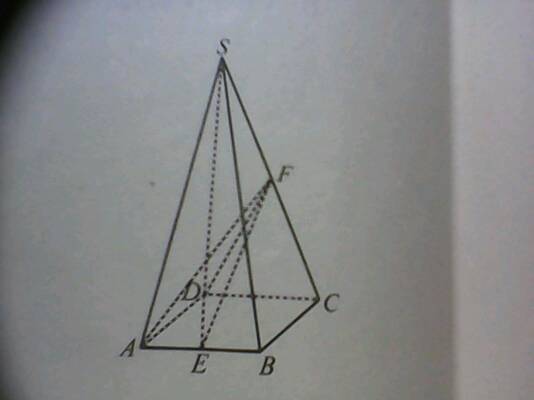



四稜錐 體積公式 體積公式推導 中文百科全書



1



Ppt 除了平面圖形以外 像下列這些在生活中常見物體的形狀都是立體圖形 Powerpoint Presentation Id




2 4 生活中的立體圖形能以最少性質辨認立體圖形 能理解柱體 錐體的頂點 面 邊的組合因素 能理解柱體 錐體的基本展開圖 Ppt Download
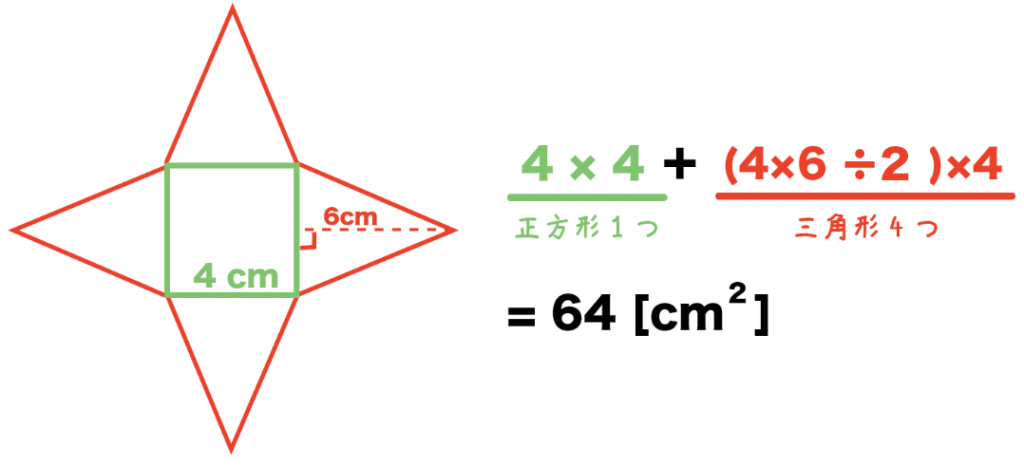



簡単公式 正四角錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



第四冊
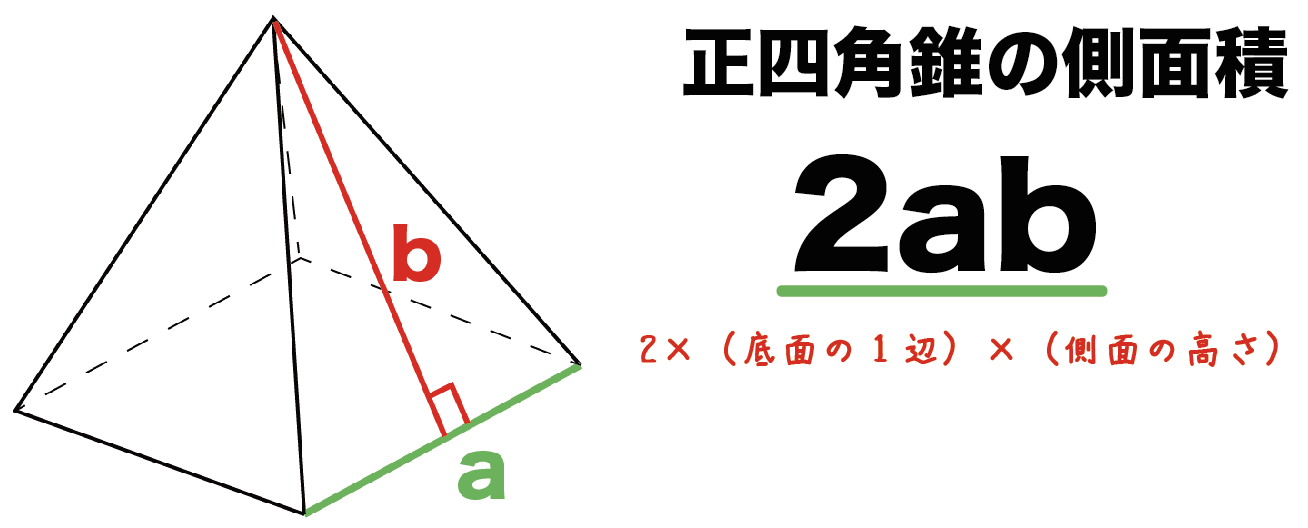



計算公式 正四角錐の側面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



Http Www Gjjh Tp Edu Tw Mediafile Fdownload 69 446 16 2 29 22 0 43 446 Nf1 Pdf




角錐 円錐の体積と表面積の公式 数学fun




球表面積公式球體表面積 百度百科 Kmbymh



1 1 負數與數線




100以上四角錐体積公式 ユニークな壁紙サイトhd
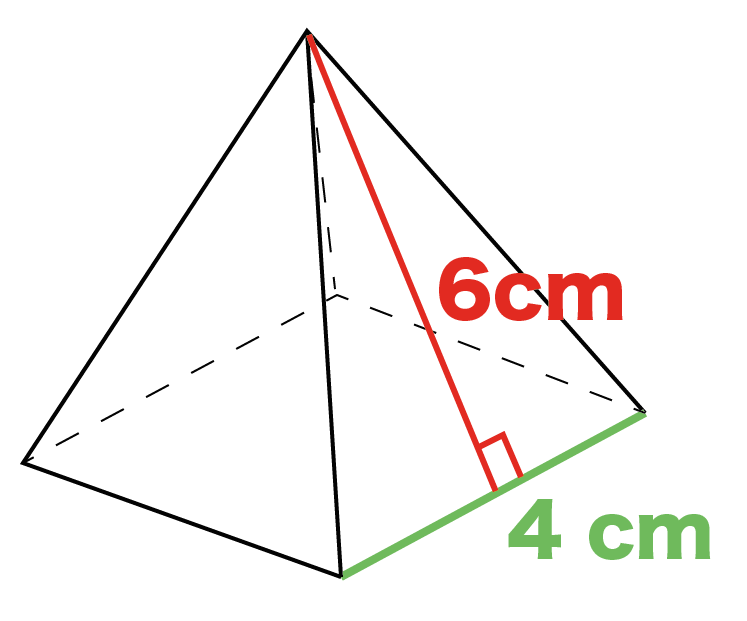



簡単公式 正四角錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



Shihmath Files Wordpress Com 18 07 Unit 15 E7ab8be9ab94e59c96e5bda2e79a84e59fbae69cace680a7e8b3aa Pdf



角錐表面積的計算實例 Live 多媒體數學觀念典online
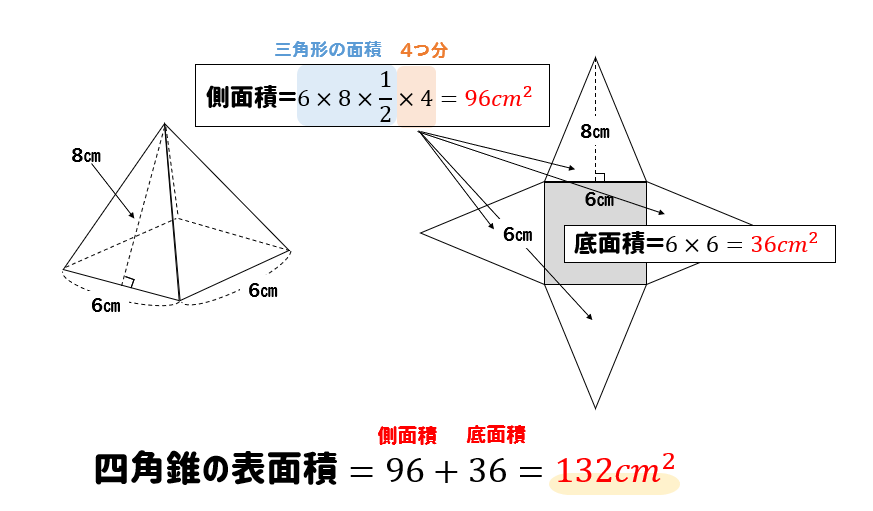



3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ




第15題求解 Clear




中3数学正四角錐の母線長頂点を共有する三角形の面積比 三角錐の体積比 05 03 Youtube



Http Local Wfsh Tp Edu Tw Bteam Curriculum Get Exam File Asp No 445




長方形面積求邊長翻轉學習影片 國小 數學 3 16 2 Mqttk




梯形面積計算方法平行四邊形 三角形和梯形的面積 Wjklv



Http Data Pakkau Edu Hk Chanpuiyee 16 17 s3 math E4 B8 Ad E4 B8 E7 B4 9a E7 Ac Ac E4 Ba 94 E7 Ab A0 E9 9d E7 8d E5 92 8c E9 Ab 94 E7 8d E4 B8 Pdf



1



四角錐台の公式 体積 側面積 表面積 数学 エクセルマニア
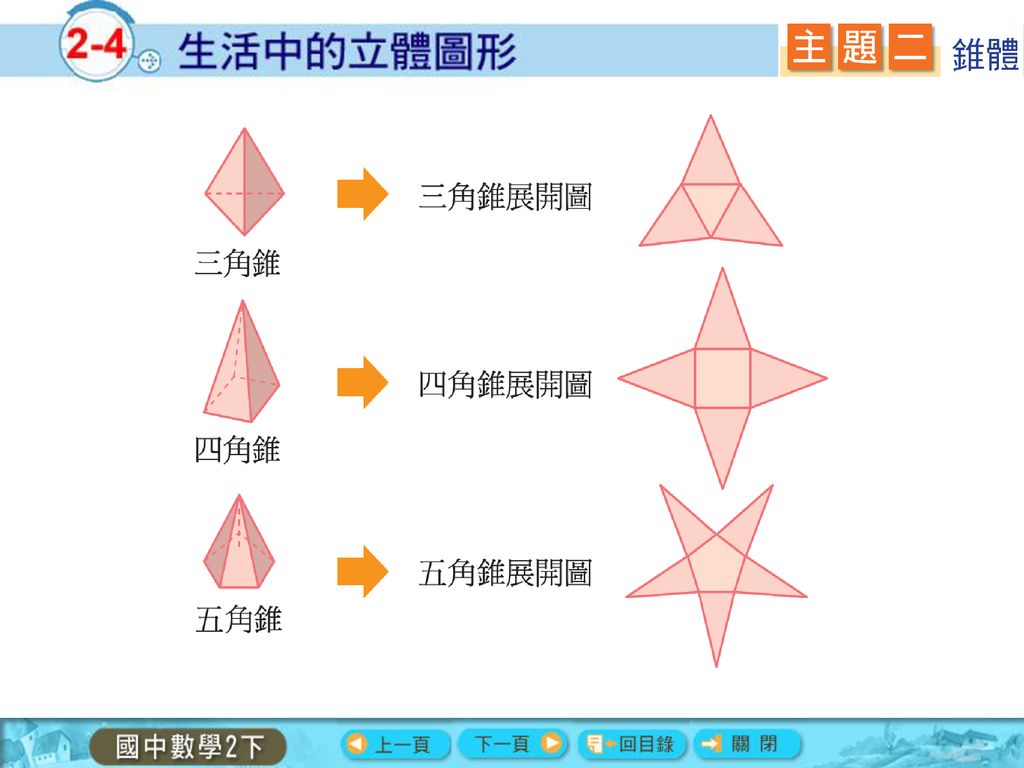



1 Boy的聲音問 Ppt Download




錐體體積 1 3柱體體積的3種證明法 Ishewh的創作 巴哈姆特



2 4 生活中的立體圖形能以最少性質辨認立體圖形 能理解柱體 錐體的頂點 面 邊的組合因素 能理解柱體 錐體的基本展開圖 Ppt Download




圓柱體曲面面積圓柱體曲面面積 Jvvx



Http Topmath Org Jtest Ex 1401 Pdf




圓錐曲面面積公式圓錐的曲面面積的副本 Pbhcl




14 平面及立體圖形 立體圖形的表面積及體積 齊齊溫




高さの分からない正四角錐の体積を求める方法をイチから解説 数スタ




四角錐の表面積の求め方 公式 小学生 中学生の勉強




正四面积体体积 表面积计算公式与在线计算器 三贝计算网 23bei Com



0 件のコメント:
コメントを投稿